機器學習(以下簡稱ML)的核心其實就是數學運算，而且只能運算特定類型的資料型式。但是在真實世界中，我們的很多資料是無法能夠立刻丟進去做數學運算的。例如，決策樹(decision tree)的數學運算 — 決策樹機器學習軟體通常還包括從資料中學習最佳樹的功能以及讀取和處理不同類型的數字和分類資料的方法。 然而，支撐決策樹的數學函數（如下圖）對boolean變量進行運算並使用諸如 AND或OR 之類的運算(如下圖)。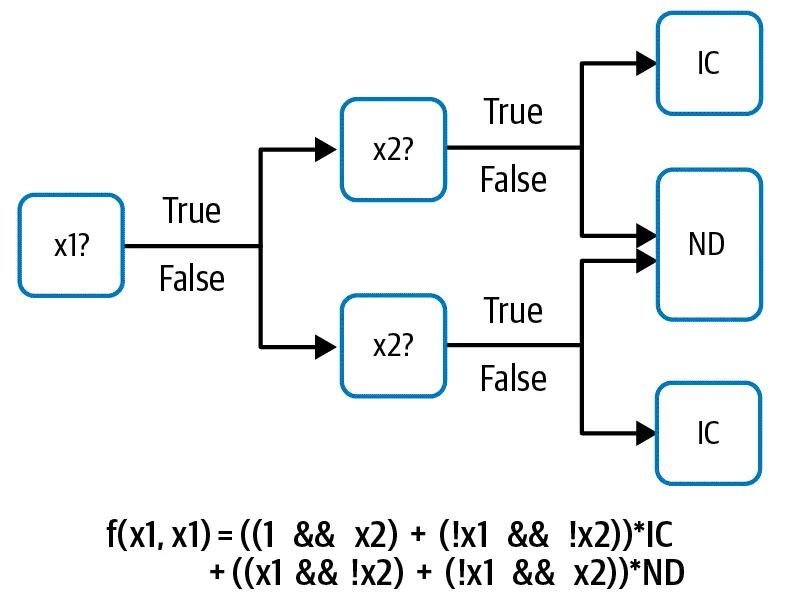

假設我們要對新生兒做出生時需要留院照護(簡稱IC)或是正常出院(簡稱ND)，而決策樹會有兩個輸入的變量，分別是x1, x2。哪麼我們的訓練模型就會如上圖。

針對這兩個x1, x2，我們考慮使用新生兒是否在醫院出生與其體重來當作輸入變量。是不是在醫院出生可以當作輸入變量嗎?答案是不行，因為這個變量只有"是(True)"與"不是(False)"兩種輸入值，這樣的輸入是boolean的AND操作無法直接運算的。因為剛剛提到ML只會做數學運算，而True / False不能直接操作的資料型態。當然我們也可以將醫院這個變量轉換成boolean AND可以操作的式子:

x1 = (醫院 IN 台北)

這樣式子就會有醫院在台北就為True，若不式就是False。同樣的，新生兒的體重也無法讓boolean AND/OR 可以直接運作，我們可以加入條件來辨識:

x1 = (新生兒體重 < 2000公克)

我們也可以使用醫院或新生兒體重的權重來當作模型的輸入值。我們可以使用醫院或新生兒體重作為模型的輸入值。 這是輸入值（醫院、複雜object或v新生兒體重、浮點數）如何以模型期望的形式（boolean）呈現的範例。這就是本文的標題 — "資料的呈現"。

本文中，我們會用輸入(input)來呈現真實世界的資料輸入(例如剛剛提到的新生兒體重)與另一個專門術語: feature來呈現經過轉換後的資料(例如低於2000公克的體重)，而這個資料是會實際被模型運作的。我們在create feature的過程稱為特徵工程(feature engineering)，我們可以想像成特徵工程就是我們選擇資料要怎麼樣的呈現。

當然，與其直接將規則寫死在我們的參數中(體重低於2000公克)，在ML的世界中我們比較傾向ML模型通過選擇輸入(input)變量和閾值(threshold)來學習如何創建每個node。決策樹是能夠學習資料呈現的ML模型的一個例子。 我們在本文中看到的許多模式將涉及類似的可學習的資料呈現。

崁入式設計模式是深度神經網路能夠自行學習的資料呈現的典型範例。在嵌入設計模式中，學習到的資料呈現比輸入更密集(dense)且維度更低，輸入可能是稀疏的(spare)。學習演算法需要從輸入中提取最顯著的資訊，並在特徵中以更簡潔的方式來呈現。學習特徵以呈現輸入資料的過程稱為"特徵提取(feature extraction)"，我們可以將可學習的資料呈現視為自動化的工程特徵。

資料呈現甚至不需要是單個輸入變量 — — 例如，傾斜決策樹通過對兩個或多個輸入變量的線性組合進行閾值化(thresholding)來創建boolean feature。每個節點只能表示一個輸入變量的決策樹簡化為逐步線性函數，而每個節點可以表示輸入變量的線性組合的傾斜決策樹簡化為分段線性函數（下圖）。考慮到需要學習多少steps才能充分表示直線，分段線性模型更簡單、更容易學習。這個想法的延伸是Feature Cross設計模式，它簡化了multivalued categorical variables與 AND 之間關係的學習。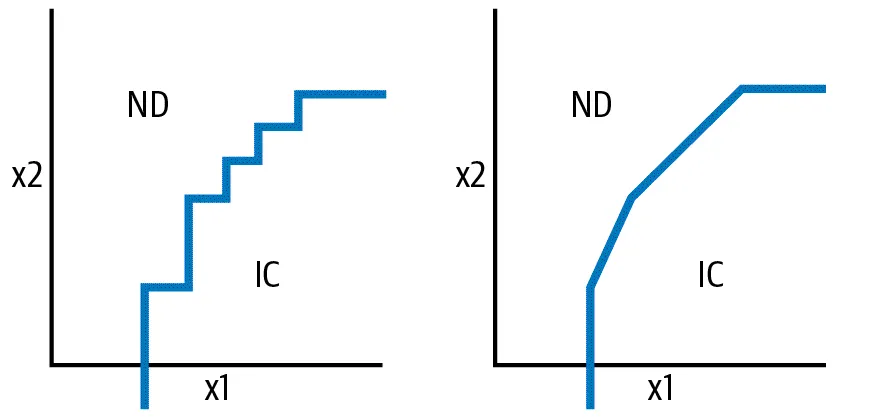

資料呈現不需要學習或固定 — — 混合也是可能的。 Hashed Feature 設計模式是確定性的，但不需要模型知道特定輸入可以採用的所有可能的值。 到目前為止我們看到的資呈現都是一對一的。 雖然我們可以分別表示不同類型的輸入資料，也可以將資料的每個部分表示為一個特徵，但使用 Multimodal Input 可能更有利。

簡單的資料呈現
在我們深入研究可學習的資料呈現、特徵交叉(feature crosses)等之前，讓我們看看其他更簡單的資料呈現。 我們可以將這些簡單的資料呈現視為ML中的常見術語——不完全是模式(patterns)，但仍然是常用的解決方案。

數字型的輸入
現代化且大規模的ML模型(如隨機森林樹，SVM，神經網路)運算的都是數字，所以這些模型的輸入(input)也是數字。

為什麼縮放(Scaling)是好用的
通常，由於 ML 框架使用優化器(optimizer)，該優化器可以很好地處理 – 1到 1 範圍內的數字，因此將數值縮放到該範圍內可能是有效益的。

哪為什麼縮放的數字會是介於 -1 到 1之間呢?
梯度下降(Gradient descent)優化器需要很多步驟(steps)才能到達loss function的谷底。這是因為具有較大相對量級的特徵(features)的導數也會趨於較大，從而導致權重(weight)的更新會變得不正常。 異常大的權重更新將需要更多的步驟來收斂，而越多steps運算的負載就會加重。 將資料“居中”到 [– 1, 1] 範圍內使誤差函數會變得更加球形。 因此，使用轉換資料訓練的模型趨於更快收斂，因此訓練(電腦運算)更快/成本更低。 此外，[– 1, 1] 範圍提供最高的浮點精度。

縮放的另一個重要原因是一些ML演算法和技術對不同特徵的相對大小非常敏感。 例如，使用歐幾里得距離作為其鄰近度度量的 k-means clustering演算法最終將嚴重依賴具有較大量級的特徵。 缺乏縮放也會影響 L1 或 L2 正則化的效果，因為特徵的權重大小取決於該特徵的值的大小，因此不同的特徵會受到正則化的不同影響。 通過將所有特徵縮放到 [– 1, 1] 之間，我們確保不同特徵的相對幅度沒有太大差異。

線性縮放(scaling)
以下為四種常用的線性縮放型式

Min-max scaling
數值是線性縮放的，因此輸入可以取的最小值縮放到 –1，最大可能值縮放到 1：

x1_scaled = (2*x1 — max_x1 -min_x1) / (max_x1- min_x1)

min-max scaling的問題在於最大與最小值(max_x1 and min_x1)的預估通常來自於訓練資料集，而這些資料通常都有"離群值"。所以真實的資料通常會被壓縮在 -1到1之間。

Clipping(剪裁 — 與min-max scaling結合)
通過使用“合理”值而不是從訓練資料集中估計最小值和最大值，幫助解決離群值的問題。 數值在這兩個合理邊界之間做線性縮放，然後裁剪到 – 1到1 範圍內。 這具有將離群值視為 –1 或 1 的效果。

Z-score 正則化
通過使用在訓練資料集上預計的平均值和標準差對輸入(input)進行線性縮放，解決了離群值問題，而無需事先了解合理範圍是多少：

x1_scaled = (x1- x1的平均值) / x1的標準差

這個方法的名稱反映了這樣一個事實，即縮放值的平均值為零並通過標準差進行正則化，因此它在訓練資料集上具有單位方差(unit variance)。 縮放值是無邊界的，但大部分時間確實在 [– 1, 1] 之間（67%，如果資料分佈是鐘型曲線的）。 超出此範圍的值的絕對值越大，它們就越少會出現，但它們仍然存在。

Winsorizing
使用訓練資料集中的經驗分佈將資料集裁剪到資料值的第 10 個和第 90 個百分位（或第 5 個和第 95 個百分位，依此類推）給出的邊界。 winsorized 值是min-max縮放。

上述提到的所有方法均屬線性縮放資料（在clipping和 winsorizing 的情況下，在正常範圍內線性）。 Min-max 和clipping往往最適均勻分佈(uniformly distributed)的資料，而 Z-score 往往最適合常態分佈(鐘型曲線)的資料。 嬰兒體重預測範例中不同縮放函數對x軸(媽媽的年齡)的影響如下圖所示

不要捨棄離群值
我們將Clipping(裁剪)定義為將小於 –1 的值並將其視為 –1，將大於 1 的值視為 1。不要丟棄此類“離群值”，因為我們期望ML模型在正式環境中會遇到這樣的離群值。以 55 歲母親所生的嬰兒為例。因為我們的資料集中沒有足夠的年長母親，Clipping最終將所有 45 歲以上的母親視為 45歲。同樣的處理將應用於正式環境，因此，我們的模型將能夠處理年長的母親.如果我們簡單地丟棄所有 55 歲以上母親所生嬰兒的訓練樣本，該模型將不會學會反映離群值。另一種思考方式是，雖然丟棄無效輸入是可以接受的，但丟棄有效資料是不可接受的。因此，我們有理由丟棄母親的年齡是負數的(年齡沒有負數)，因為這可能是資料輸入錯誤。在正式環境中，輸入資料的驗證將確key in的人必須重新輸入母親的年齡。然而，我們沒有理由丟棄 母親年齡為 55 的資料，因為 55歲 是一個完全有效的輸入，並且一旦模型部署到正式環境中，我們預計將會遇到 55歲甚至年齡更大的母親歲數。

在下圖中，我們可以注意到 minmax_scaled(右上角) 使 x value進入所需的 – 1到 1 範圍內，但在曲線的最末端我們並沒有足夠的資料顯示這些極端值。 Clipping匯總了許多有問題的value，但需要使clipping閾值(thresholds)完全正確 — — 在這裡，40 歲以上母親的嬰兒數量緩慢下降，這給設定hard thresholds帶來了問題。 Winsorizing 與Clipping類似，需要使百分位數閾值完全正確。 Z-score 正則化改進了範圍（但不會將值限制在 [– 1, 1] 之間）並將有問題的值推得更遠。 在這三種方法中，zero-norming最適用於預估母親年齡與新生兒關係間的這個問題，因為年齡的raw data有點像鐘形曲線。 對於其他問題，min-max scaling、Clipping或 winsorizing 可能更適合。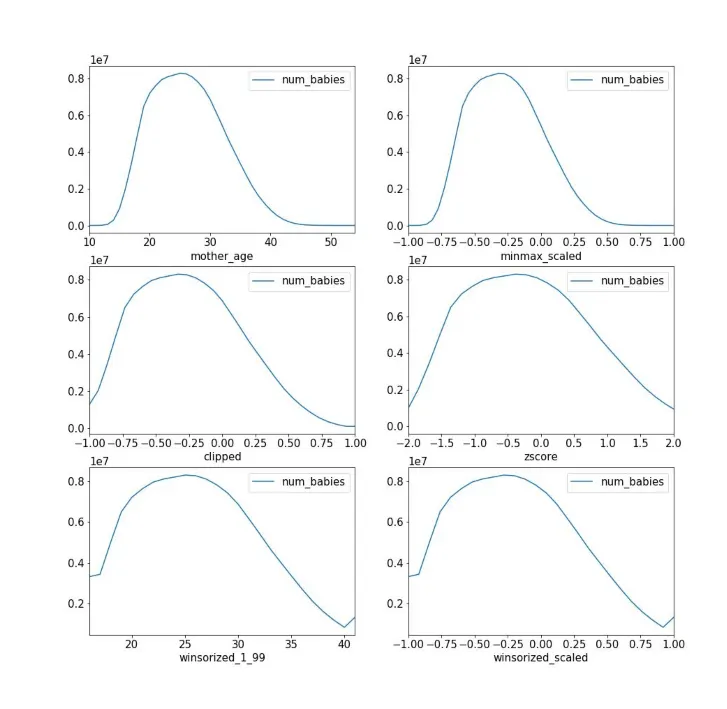

非線性轉換(Nonlinear transformation)
如果我們資料在呈現時是偏斜的並且不是均勻分布也不是鐘形曲線呢?這一類的狀況，解決的方法是在Scaling之前，將非線性轉換apply到input。一種常見的技巧是在Scaling之前取input value的對數。 其他常見的變換包括 sigmoid 和多項式的展開（平方、平方根、立方、立方根等）。 如果轉換後的值的分佈變得均勻或正態分佈，我們就會知道我們有一個很好的轉換函數。

假設我們要建立一個模型來預測一本科幻小說的銷售。其中一個資料input是與這本小說主題有對應到的維基百科頁面的瀏覽數。然而，維基百科頁面的瀏覽量是高度偏斜的，並且佔據了很大的資料範圍（見下圖 左一圖：資料分佈高度偏向於很少瀏覽的頁面，但最常見的頁面被瀏覽了幾千萬次）。 通過取views的對數，然後取這個對數值的四次方根並線性縮放經過四次方的結果，我們得到了一些在所需範圍內並且有點呈現鐘形曲線的東西。

上圖中(左一)維基百科頁面瀏覽量分佈高度偏斜，資料範圍較大。 左二途展示了可以通過使用對數、冪函數和連續線性縮放轉換view number來解決問題。 第三個圖顯示直方圖均衡化的效果，第四個圖則顯示 Box-Cox 轉換的效果。

設計一個使分佈看起來像鐘形曲線的線性化函數可能很困難。 一種更簡單的方法是將視圖數量bucketize，選擇bucket邊界以適合所需的輸出分佈。 選擇這些bucket的原則方法是進行直方圖均衡化(histogram equalization)，其中直方圖的bucket是根據原始分佈的分位數選擇的（如上圖 左三）。 在理想情況下，直方圖均衡會導致均勻分佈（儘管在這種情況下並非如此，因為分位數中有重複值）。

另一種處理分布高度偏斜的技術是使用 parametric transformation，例如 Box-Cox 轉換。Box-Cox 選擇其單個參數 lambda 來控制“異方差性(heteroscedasticity)”，以便方差不再取決於幅度(magnitude)。 在這裡，很少查看的維基百科頁面之間的差異將遠小於經常查看頁面之間的差異，Box-Cox 試圖在所有查看次數範圍內均衡差異。

矩陣型數字(Array of numbers)
我們有時遇到的輸入資料會是矩陣型的數字。假設矩陣內的數字是固定長度，資料的呈現就相對簡單: flatten這個矩陣並將每個position視為一個單獨的feature。不過通常的狀況都是矩陣是非固定的。例如，我們一樣要預測科幻小說的銷售數量，這一次的input則是擁有相同主題其他小說的歷史銷售量。假設資料如下:

[3100, 16500, 270000, 2000, 100, 769330]

很顯然我們看到這個array中的每個value差異很大。我們會用一些常見慣用語來處理array of numbers,包含如下:

• 根據批量統計資料呈現input array。 例如，我們可能會使用長度（即之前關於該主題的書籍的數量）、平均值、中位數、最小值、最大值等。
• 根據經驗分佈呈現input array — — 即，按第 10/20/… 百分位數，依此類推。
• 如果array 以特定方式排序（例如，按時間或大小排序），則按最後三個或其他固定數量的項目呈現input array 。

所有這些最終都將可變長度的資料array 呈現為固定長度的特徵。 我們也可以將這個問題描述為時間序列預測問題，即根據前一本書的銷售時間歷史預測該主題下一本書的銷量的問題。 通過將以前書籍的銷量視為array input，我們假設預測一本書銷量的最重要因素是書籍本身的"特徵"（例如:作者、出版商、評論等），而不是帶有著時間連續性的銷售總額。

分類輸入(Categorical Inputs)
現代化且大規模的ML模型(隨機森林樹，SVM，神經網路)都是數字類的value，所以分類式的資料也必須用數字來代替。

簡單地列舉可能的Value並將它們映射到一個ordinal scale將會處理得很差。 假設預測科幻小說類書籍銷量的模型的inpute之一是這本書的語言版本。 我們不能就這樣建立這樣的mapping table(如下圖)：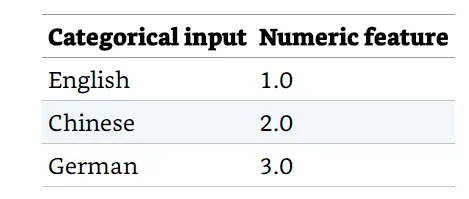

這是因為ML模型會嘗試在德語和英語書籍的受歡迎度之間進行插值(interpolate)，以獲得中文書籍的受歡迎度。因為語言之間沒有序數(ordinal)關係，我們需要將分類對映到數字，讓模型能夠獨立學習用這些語版本書籍的市場。

One-hot encoding
在確保變量(variables)獨立的同時對映分類變量的最簡單方法是one-hot encoding。 在我們的下面的範例中，分類輸入變量將使用以下對映為三個元素特徵向量：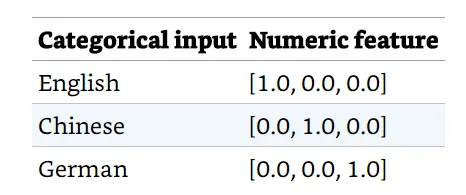

One-hot encoding 要求我們事先要知道分類輸入的詞彙表。 在這裡，詞彙表由三個標記（英語、中文和德語）組成，生成的特徵的長度就是這個詞彙表的大小。

Dummy coding or One-hot encoding?
技術上，兩個元素的特徵向量也足夠呈現我們的範例，如下圖: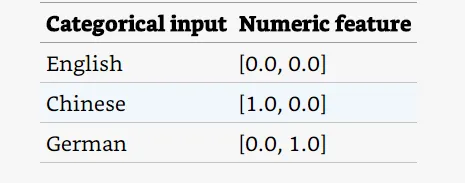

這個方式稱為Dummy coding，因為dummy coding是一種更嚴謹的呈現，所以當input是無關線性時，它在效能更好的統計模型中是首選。 然而，現代ML演算法並不要求它們的input是無關線性，而是使用 L1 正則化等方法來修剪redundant inputs。 額外的自由度允許框架透明地將真實環境中missing input都視為零的資料，因此許多ML框架通常只支援one-hot encoding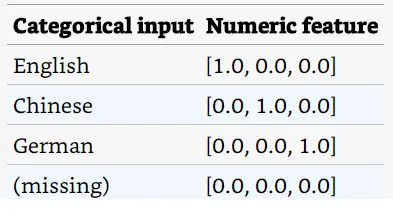

在某些情況下，將分類型資料看成是數字型資料並對映到one-hot encoding column是有幫助的:

當數字型的input是一個index時
例如，如果我們試圖預測交通流量並且我們的inputs之一是一周中的星期幾，我們可以將星期幾視為數字 (1, 2, 3, …, 7)，但它有助於認識到這裡的星期幾不是連續的數字，而實際上只是一個index。 所以最好將其視為分類（星期日、一、……、六），因為index是arbitrary。 一周應該從星期日（如美國）、星期一（如台灣）還是星期六（如埃及）為開始？

當input與label之間的關係是不連續的
將星期幾作為分類特徵的評估應該傾向的是周五的交通流量不受週四和周六的影響。

當對數字變量(variable)進行bucket是有利的時
在大多數的城市，交通流量變化分界在於是不是處在周末的時間，而且每個城市的狀況還可能不一樣(有些週六日算周末，有些可能是週四跟周五 — 像是伊斯蘭國家)。這種是不是周末或不是周末的分別，很適合用boolean feature。這種不同input的數量（此處為 7）大於不同特徵值的數量（此處為 2）的映射稱為bucketing。 通常，bucketing是根據range進行的 — — 例如，我們可能將 母親的年齡分入在 25、30、35等處中斷的範圍，並將這些 bin 中的每一個都視有分類的，但我們要意識到這樣做等於失去了ordinal性質的母親的年齡。

當我們想要將數字的input的不同value視為獨立時，當它們對label產生影響時。
例如，嬰兒的體重取決於分娩的次數，因為雙胞胎和三胞胎的體重往往低於一胎。 因此，如果是三胞胎的一部分，體重較輕的嬰兒可能比體重相同的雙胞胎嬰兒更健康。 在這種情況下，我們可以將複數對映到一個分類變量，因為分類變量允許模型為複數的不同value學習獨立的可調參數。 當然，只有在我們的資料集中有足夠多的雙胞胎和三胞胎的資料時，我們才能做到這一點。

分類型變量的陣列(array)
我們之前提到陣列的資料長度通常是多變的。如果我們有一個陣列來呈現母親生產的方式

[Induced, Induced, Natural, Cesarean]

而通常我們常用來處理分類型變量陣列的資料如下:

• 計算每個詞彙item的出現次數。 因此，假設詞彙是誘導(Induced)、自然(Natural)和剖腹產(Cesarean)（按此順序），我們範例資料的呈現將是 [2, 1, 1]。 現在這是一個固定長度的數字array，可以按位置順序攤平和使用。 如果我們有一個array，其中一個item只能出現一次（例如，一個人說的語言），或者如果該特徵僅表示"是或不是"而不是計算它（例如母親是否曾經做過剖腹產手術），那麼計算每個位置為 0 或 1，這稱為multi-hot encoding。
• 為避免大的數字，可以使用相對頻率代替計數。 我們範例資料的呈現將是 [0.5, 0.25, 0.25] 而不是 [2, 1, 1]。 Empty arrays（沒有兄弟姐妹的第一個出生的新生而）表示為 [0, 0, 0]。 在自然語言處理中，單詞(a word)的整體相對頻率通過包含該單詞的文件的相對頻率進行歸一化，以產生 TF-IDF(first-born babies with no previous siblings)。 TF-IDF 反映了一個詞(word)對於文件的唯一性。
• 如果array以特定方式（例如，按時間順序）排序，則通過最後三個項目呈現input array。 少於三個的array用missing values代替。
• 通過批量統計來呈現array，例如array的長度、眾數、中位數、第 10/20/… 百分位數等。

其中，counting/relative-freqency慣用語是最常見的。 請注意，這兩個都是 one-hot encoding的一般化(generalization) — — 如果新生兒沒有哥哥姐姐，則表示將是 [0, 0, 0]，如果新生兒有一個自然出生的哥哥姐姐， 表示將是 [0, 1, 0]。 看過簡單的資料呈現後，將有助於我們討論資料呈現的設計模式。